LEGO elements have their own geometry. Let's start simple. 3 plates stacked on top of each other are as high as a standard LEGO brick.
LEGOmetry – the geometry of LEGO bricks (Building Technology)
If not only bricks or plates are stacked on top of each other, SNOT is involved. The studs are facing different directions but everything should be held together without gluing and it should look smooth without any gaps. Therefore we have to consider the ratio between the thickness of plates and the width of studs.
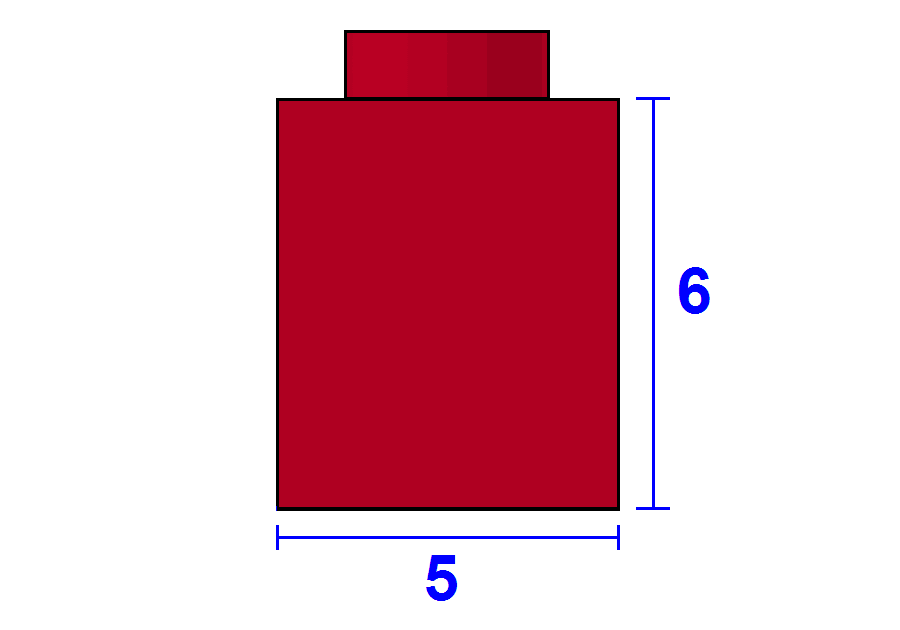
Stacking 5 plates on top of each other makes them as high as the width of a 1x2 brick.
5:6 ratio
This characteristic of the height of plates and the width of bricks is called the 5:6 ratio (say "five to six") of LEGO bricks.
This 5:6 ratio becomes clear if you want to build a square or cube, a shape with equally long edges.
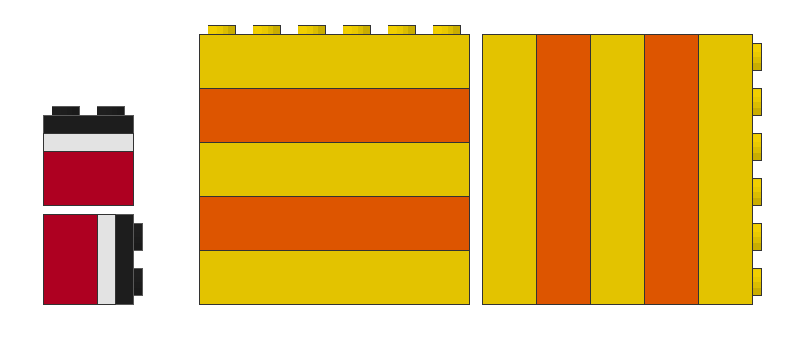
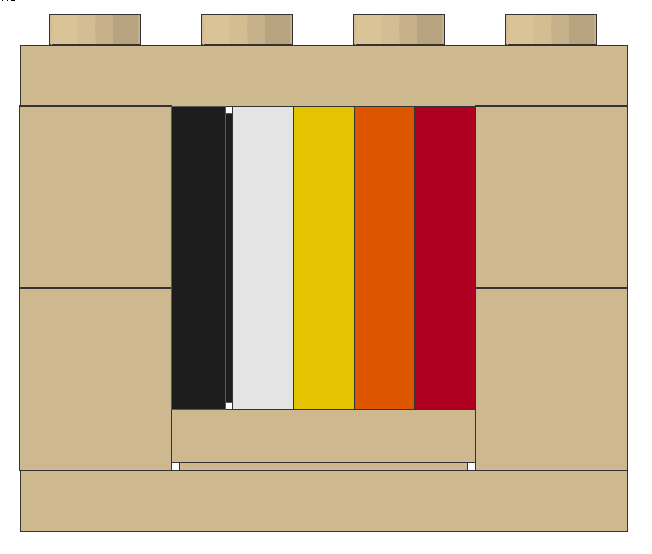
A square occurs if a 1x2 brick and two 1x2 plates are stacked on each other. Ok, the studs are outside of this square. But maybe they are needed to fix the square somehow?
A square also could be build by stacking five 1x6 bricks on top of each other.
Such a square can be fully fitted in a surrounding construction. This technique is used to realise various colours of strips or even letters.
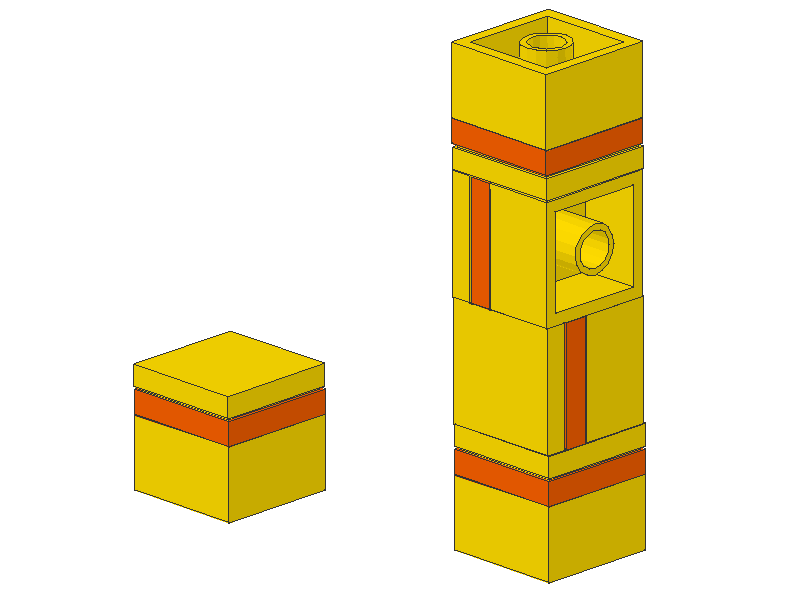
A cube is a construction with equally long edges. Using LEGO such a cube can be build by a 2x2 brick, a 2x2 plate and a 2x2 tile. Using this technique, I build parts of the outer facade of my Frauenkirche. The challenge now is to hold all these cubes together which could face in various directions.
But SNOT will help in this case …
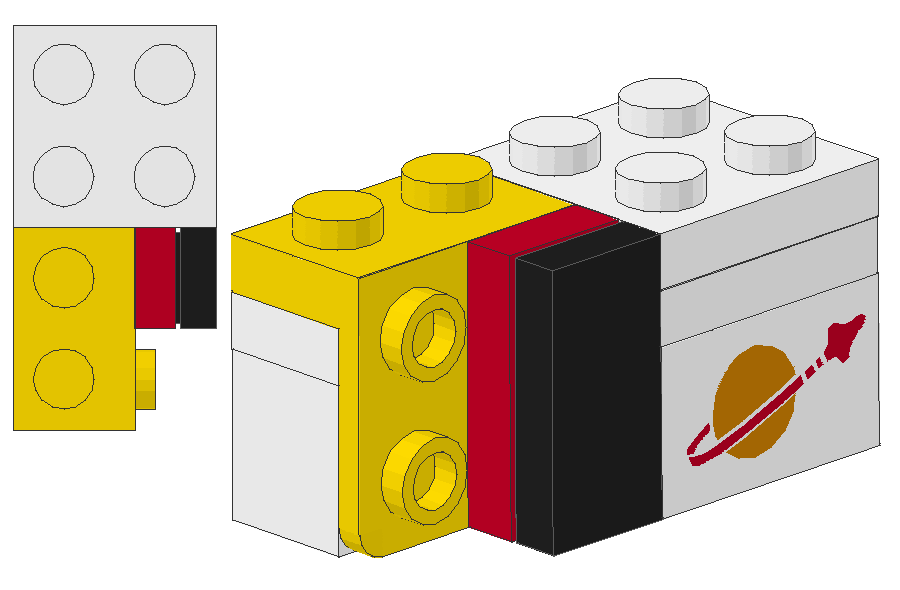
The SNOT converteres show a slightly different geometry then standard bricks and plates. The upright plate at various brackets is much thinner then a standard plate. But together with a normal plate and a tile everyting is as wide as a standard brick. Using this technique allows to attach elements SNOT wise into a wall without anything outstanding from the wall.
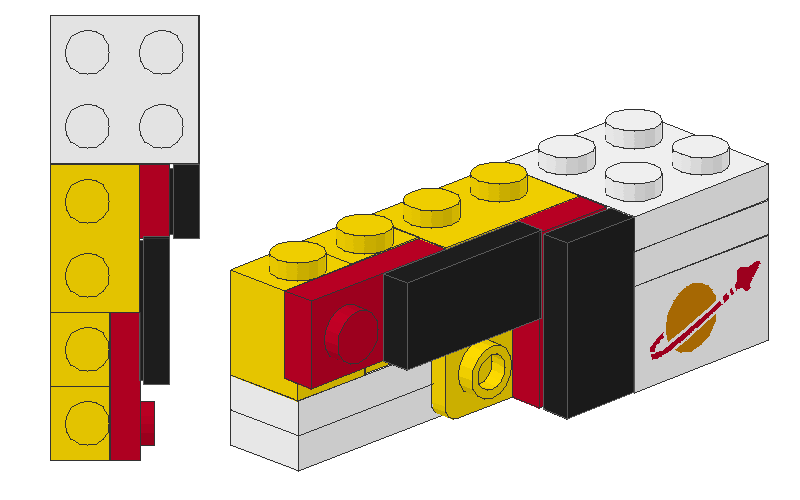
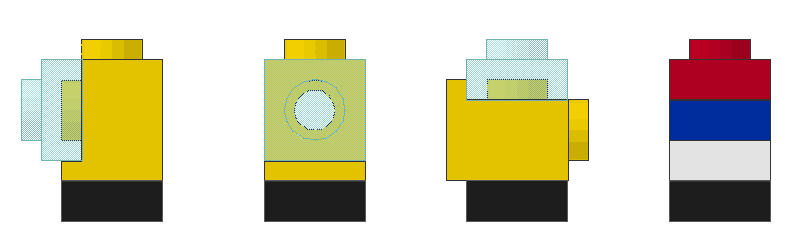
Headlight bricks and the much newer SNOT converter fit together nicely.
Headlight bricks
The headlight bricks become even more interesting if you discover their own geometry | more